جواب فصل هفتم ۷ ریاضی پنجم (آمار و احتمال)

پاسخ درس هفتم ریاضی پایه پنجم (آمار و احتمال)

راهنمای کامل حل تمرین‌های فصل هفتم

در این بخش، به تمام پرسش‌ها و تمرین‌های درس «آمار و احتمال» پاسخ داده می‌شود. هدف این است که مفاهیم اصلی این درس را به طور کامل و مرحله به مرحله فرا بگیرید.

مطالب این درس حول دو محور اصلی می‌چرخد:
1. **آمار:** که دربارهٔ جمع‌آوری اطلاعات، دسته‌بندی و نمایش آن‌ها به روش‌های مختلف مانند نمودار میله‌ای است.
2. **احتمال:** که به ما کمک می‌کند شانس رخ دادن یک اتفاق را پیش‌بینی کنیم.

برای هر سوال، راه حل به صورت واضح و مرحله به مرحله ارائه شده است. با دنبال کردن این راهنما می‌توانید درک درستی از چگونگی تحلیل داده‌ها و محاسبهٔ احتمال به دست آورید. این راهنما به شما کمک می‌کند تا خودتان برای حل مسائل مشابه آماده شوید.

درس: آمار و احتمال
مبحث: یادگیری مرحله به مرحله
پایه: پنجم دبستان

در این درس، با مفاهیم اولیه آمار و احتمال آشنا می‌شویم. هدف این است که بتوانیم اطلاعات ساده را جمع‌آوری و دسته‌بندی کنیم و سپس با استفاده از این اطلاعات، نتیجه‌گیری‌های کوچک و منطقی داشته باشیم.

برای شروع، یاد می‌گیریم که چگونه چیزهای مختلف را در گروه‌های مرتب قرار دهیم. مثلاً اگر چند مدل میوه داشته باشیم، می‌توانیم آن‌ها را بر اساس نوع، رنگ یا اندازه دسته‌بندی کنیم. این کار به ما کمک می‌کند تا اطلاعات را راحت‌تر بفهمیم.

سپس سراغ ساختن نمودارهای ساده می‌رویم. نمودار میله‌ای یک روش آسان و تصویری برای نشان دادن اطلاعات است. با کشیدن نمودار، می‌توانیم به سادگی ببینیم که کدام گروه تعداد بیشتری دارد یا کدام یک کمتر است.

در بخش احتمال نیز می‌آموزیم که چگونه رویدادهای ساده را پیش‌بینی کنیم. احتمال به ما می‌گوید که چقدر احتمال دارد یک اتفاق رخ دهد. مثلاً وقتی یک سکه را به هوا پرتاب می‌کنیم، احتمال اینکه رو بیاید یا پشت، برابر است. این بخش مانند یک بازی فکری است که به ما کمک می‌کند حدس‌های منطقی بزنیم.

در پایان این درس، شما می‌توانید داده‌های ساده را جمع‌آوری و مرتب کنید، آن‌ها را به صورت نمودار نشان دهید و درباره احتمال وقوع اتفاقات کوچک، پیش‌بینی‌های ساده داشته باشید.

گام به گام درس هفتم ریاضی پنجم ابتدایی

راهنمای فصل هفتم ریاضی پنجم دبستان
پاسخ به تمرین‌ها و فعالیت‌های صفحات ۱۲۶ تا ۱۳۹

فهرست دسترسی سریع:
– پاسخ فعالیت صفحه ۱۲۶
– پاسخ کار در کلاس صفحه ۱۲۷
– پاسخ فعالیت صفحه ۱۲۸
– پاسخ صفحه ۱۲۹
– پاسخ فعالیت صفحات ۱۳۰ و ۱۳۱
– پاسخ کار در کلاس صفحه ۱۳۱
– پاسخ فعالیت صفحه ۱۳۲
– پاسخ تمرین صفحه ۱۳۳
– پاسخ فعالیت صفحه ۱۳۴
– پاسخ کار در کلاس صفحه ۱۳۵
– پاسخ فعالیت صفحه ۱۳۶
– پاسخ کار در کلاس صفحه ۱۳۶
– پاسخ تمرین صفحه ۱۳۷
– پاسخ بخش “فرهنگ نوشتن” صفحات ۱۳۸ و ۱۳۹

در این بخش، پاسخ کامل تمام سوالات و تمرین‌های فصل هفتم کتاب ریاضی پایه پنجم ارائه شده است.

جواب فعالیت صفحه ۱۲۶ فصل هفتم ریاضی پنجم دبستان

پویا از بچه‌ها پرسید که در روزهای تعطیل معمولاً چقدر وقت برای بازی می‌گذارند. سپس پاسخ هر یک از دوستانش را در یک جدول مرتب کرد. به این اطلاعاتی که جمع‌آوری می‌شود، «داده» می‌گویند و به جدولی که این اطلاعات در آن ثبت می‌شود، «جدول داده‌ها» گفته می‌شود.

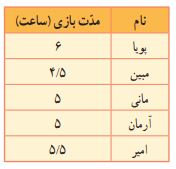
الف) کدام یک از بچه‌ها زمان بیشتری را به بازی اختصاص می‌دهد؟ پویا
ب) کدام یک کمتر بازی می‌کند؟ مبین
پ) بین اعداد موجود، کدام یک بیش‌تر از بقیه دیده می‌شود؟ عدد ۵ (که دو بار آمده است)
ت) مانی و مبین هر کدام یک نمودار ستونی بر اساس اطلاعات جدول کشیده‌اند. با دقت به این نمودارها نگاه کنید.
عنوان هر نمودار و نام‌های محورهای افقی و عمودی آن را بخوانید.

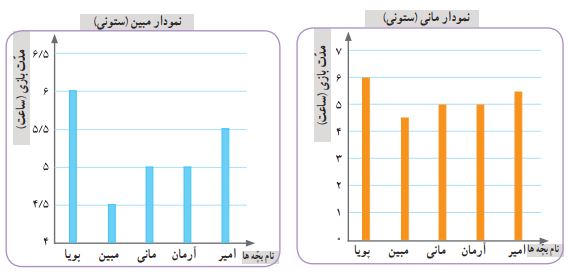
مقایسه نمودارهای مبین و مانی را انجام دهید. چه چیزهایی در این دو نمودار متفاوت است و چه چیزهایی شبیه به هم هستند؟

تفاوت: در نمودار مبین، اعداد روی محور عمودی از شماره ۴ آغاز می‌شوند، اما در نمودار مانی، اعداد از صفر شروع می‌شوند.

شباهت: هر دو نمودار از نوع ستونی هستند و اطلاعات یک مجموعه داده را نشان می‌دهند.

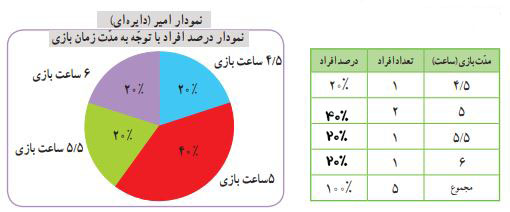
امیر با استفاده از جدول زیر، یک نمودار جدید کشیده است.

پ) جدول زیر را تکمیل کنید.

جواب کار در کلاس صفحه ۱۲۷ فصل ۷ ریاضی پنجم دبستان

نمایشگاه بین‌المللی کتاب تهران همه‌ساله در ماه اردیبهشت برپا می‌شود. آقای بهاری در دوره قبلی این نمایشگاه، یک غرفه برای فروش بستنی راه‌اندازی کرده بود. او هر روز مقدار فروش خود را ثبت و یادداشت می‌نمود. نموداری که در ادامه می‌بینید، توسط آقای بهاری برای نشان دادن میزان فروش در یکی از روزهای فعالیتش ترسیم شده است.

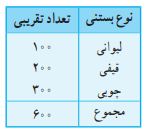
بر اساس جدولی که مشاهده می‌کنید، لطفاً نمودار دایره‌ای روبرو را تکمیل کنید.
هر بخش از این دایره، معادل ۱۰۰ عدد بستنی می‌باشد.

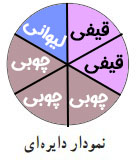
ب) به نظر شما ثبت این اطلاعات چه کمکی به آقای بهاری می‌کند؟
با استفاده از این اطلاعات، او می‌تواند بفهمد کدام نوع بستنی مشتریان بیشتری دارد و کدام نوع کمتر مورد استقبال قرار گرفته است.

دانش‌آموزان پایه‌های پنجم و ششم یک محله، در کلاس‌های آموزشی سفال‌سازی و نجاری که در سرای محله برگزار می‌شود، نام‌نویسی کرده‌اند. آمار مربوط به هر کلاس در نمودارهای زیر نشان داده شده است.
در هر کدام از این دوره‌ها ۴۰ نفر ثبت‌نام کرده‌اند. دانش‌آموزان کلاس پنجمی در کدام یک از این کلاس‌ها بیشتر نام‌نویسی کرده‌اند؟ در کلاس نجاری.

در نمودار دایرهای، هر بخش از دایره نشان‌دهنده سهم یک داده از کل اطلاعات است.

جواب فعالیت صفحه ۱۲۸ فصل ۷ ریاضی پنجم دبستان

سارا اطلاعات جدول مقابل را از پایگاه اینترنتی سازمان هواشناسی دریافت کرده است. این اعداد نشان‌دهنده بیشترین دمای ثبت‌شده در شهر کرمان طی هفت روز گذشته می‌باشد.

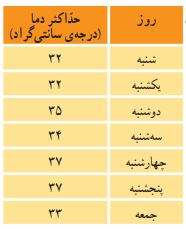
سارا تصمیم دارد یک نمودار خطی از اطلاعات خود بکشد.
الف) لطفاً خطوط افقی و عمودی نمودار او را کامل کنید.
ب) طبق دستورهای زیر، کار کشیدن نمودار را ادامه دهید:
– قسمت‌هایی که دما زیاد می‌شود را با رنگ قرمز بکشید.
– قسمت‌هایی که دما کم می‌شود را با رنگ آبی نشان دهید.
– بخش‌هایی که دما ثابت است و تغییر نمی‌کند را با رنگ مشکی رسم کنید.

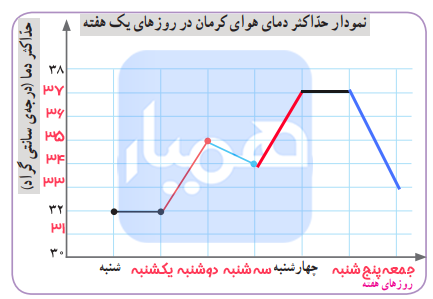
از شنبه تا یکشنبه، مقدار ثابت ماند و تغییری نکرد.
از یکشنبه تا دوشنبه، شاهد افزایش بودیم.
از دوشنبه تا سه‌شنبه، مقدار کاهش پیدا کرد.
از سه‌شنبه تا چهارشنبه، دوباره افزایش داشتیم.
از چهارشنبه تا پنج‌شنبه، مقدار بدون تغییر باقی ماند.
از پنج‌شنبه تا جمعه، کاهش مشاهده شد.

در آستانه عید نوروز، وقتی مادرش در حال سبز کردن سبزه عید بود، محیا هم یک دانه لوبیا داخل یک گلدان کوچک کاشت. او سپس رشد آن را زیر نظر گرفت و تغییراتش را در روزهای مختلف، مثل روز دوم و چهارم، یادداشت کرد.

محیا هر دو روز یکبار، قد گیاهش را اندازه می‌گرفت و آن را یادداشت می‌کرد. سپس این اطلاعات را در یک جدول مرتب کرد و با کمک آن، نمودار خطی که می‌بینید را کشید.

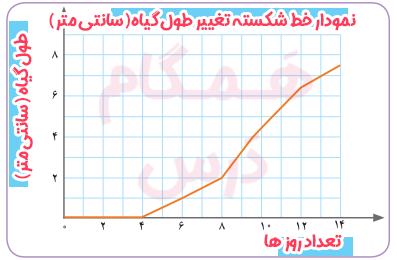
الف) عنوان‌های مناسب برای نمودار و محورهای آن انتخاب کنید.
ب) بین کدام دو روز، رشد گیاه از همه بیشتر بوده است؟ این بخش از نمودار را مشخص کنید.
بین روز هشتم تا روز دهم.

جواب صفحه ۱۲۹ فصل هفتم ریاضی پنجم

برای جمع‌آوری اطلاعات، راه‌های گوناگونی در دسترس است؛ مانند نگاه کردن، پرسیدن، استفاده از برگه‌های پرسش، مراجعه به کتاب‌ها یا پایگاه‌های اینترنتی و سنجش مقدارها.
برای هر یک از موارد زیر، چه روشی برای گردآوری اطلاعات مناسب است؟

الف) تعداد خواهر و برادرهای هر دانش‌آموز کلاس → پرسشنامه
ب) فاصلهٔ هر سیارهٔ منظومهٔ شمسی از خورشید → مراجعه به کتاب‌ها یا سایت‌ها
پ) تعداد دانش‌آموزانی که صبح با کلاه به مدرسه می‌آیند → مشاهده کردن
ت) مقدار بارندگی یک شهر در هر ماه از سال → اندازه‌گیری
ث) فعالیت‌های خارج از مدرسهٔ هر دانش‌آموز و زمان اختصاص‌یافته به هر فعالیت → پرسیدن
ج) سهم هر یک از گازهای موجود در هوا → مراجعه به کتاب‌ها یا سایت‌ها

برای نمایش اطلاعات نیز می‌توان از جدول، نمودار ستونی، نمودار تصویری، نمودار خط‌شکسته، نمودار دایره‌ای و روش‌های دیگر استفاده کرد.
به نظر شما برای نمایش اطلاعات هر موضوع در بخش قبل، کدام نوع نمایش مناسب است؟

– نمودار ستونی
– جدول داده‌ها یا نمودار تصویری
– نمودار ستونی
– نمودار خط‌شکسته
– نمودار دایره‌ای
– نمودار دایره‌ای

در اینجا اطلاعاتی درباره میزان برق مصرفی خانه‌ها در ایران طی ده سال گردآوری شده و به صورت جدول ارائه می‌شود. برای نمایش این اطلاعات به شکل یک نمودار خطی، لازم است یک مقیاس مناسب و یک نقطه شروع خوب برای محورهای نمودار خود انتخاب کنید.

فاطمه تصمیم گرفت بفهمد دانش‌آموزان چقدر با شماره‌های تلفن ضروری آشنا هستند. او یک پرسشنامه تهیه کرد و از ۲۰ دانش‌آموز خواست به سوالات آن پاسخ دهند. پس از جمع‌آوری پاسخ‌ها، نتایج را در یک جدول مرتب کرد.

الف) حالا باید یک نمودار ستونی بکشید که نشان دهد چند نفر از دانش‌آموزان هر یک از شماره‌های ضروری را بلد هستند.
(به خاطر داشته باشید که برای محور افقی و عمودی عنوان مناسب انتخاب کنید.)

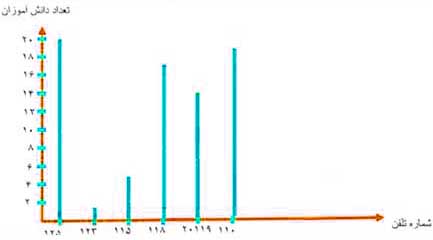
خیر، استفاده از نمودار خط شکسته برای این داده‌ها مناسب نیست. چون هدف از رسم این نمودار، نشان دادن تغییرات و نوسانات در طول زمان نیست. در واقع در اینجا قصد نداریم ببینیم که یک چیز چگونه تغییر کرده است.

جواب فعالیت صفحه ۱۳۰ و ۱۳۱ ریاضی پنجم دبستان

با استفاده از تعدادی حلقه، دو ستون در مقابل هم ساخته‌ایم. هدف این است که با همان تعداد حلقه، دو ستون بسازیم که ارتفاع یکسانی داشته باشند.
دو روش از طرف دانش‌آموزان ارائه شده است. یکی از این روش‌ها را انتخاب کنید و با کمک آن، جواب مسئله را پیدا کنید.

یکی از این روش‌ها را انتخاب کن و با استفاده از آن، جواب مسئله را پیدا کن.

_ در شکل سمت راست، تمام حلقه‌ها را از ستون‌ها بیرون بیاور. سپس در هر مرحله، همزمان در هر ستون یک حلقه قرار بده. این کار را ادامه بده تا همه‌ی حلقه‌ها داخل ستون‌ها قرار بگیرند.

_ در شکل سمت چپ، از ستونی که تعداد حلقه‌هایش بیشتر است، یکی یکی حلقه‌ها را به ستون دیگر منتقل کن. این کار را آنقدر تکرار کن تا تعداد حلقه‌ها در هر دو ستون برابر شود.

٢ــ در یک کارخانه که آبمیوه طبیعی تولید می‌کند، میزان آبی که از شش عدد سیب گرفته شده، اندازه‌گیری و در جدول زیر نوشته شده است.

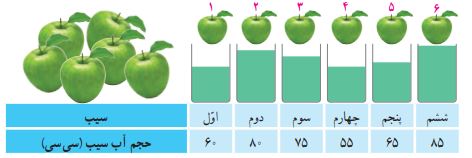
برای به دست آوردن میانگین حجم آب موجود در شش سیب، ابتدا حجم آب هر یک از سیب‌ها را با هم جمع می‌کنیم. سپس حاصل این جمع را بر تعداد سیب‌ها، که شش عدد است، تقسیم می‌کنیم. به این ترتیب، مقدار متوسط آب هر سیب محاسبه می‌شود.

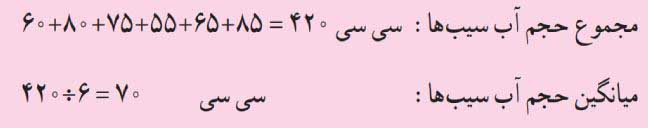
به شکل‌های زیر با دقت نگاه کنید. سپس توضیح دهید چطور می‌توان با کمک این نمودارها، میانگین مقدار آب موجود در این شش سیب را محاسبه کرد.

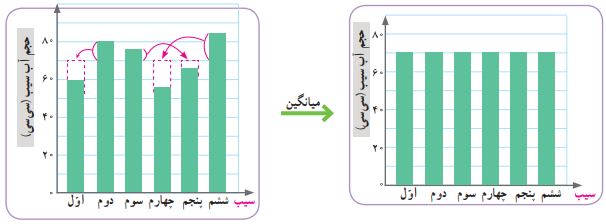
برای محاسبه میانگین داده‌ها از روی نمودار ستونی، باید ارتفاع همه ستون‌ها را با هم برابر کنیم. وقتی ارتفاع ستون‌ها یکسان شد، ارتفاعی که به دست می‌آید، همان میانگین داده‌ها خواهد بود. در نموداری که حجم آب سیب‌ها را نشان می‌دهد، بعد از این کار، ارتفاع هر ستون برابر با ۷۰ سی‌سی می‌شود. پس میانگین حجم آب هر سیب، ۷۰ سی‌سی است.

پ) یک کارخانه آب‌میوه می‌خواهد آب سیب را در بطری‌های ۷۰۰ سی‌سی بسته‌بندی کند. به نظر شما برای پر کردن هر بطری، تقریباً چند سیب لازم است؟ دلیل خود را بیان کنید.

با توجه به اینکه میانگین حجم آب هر سیب ۷۰ سی‌سی است، برای پر کردن یک بطری ۷۰۰ سی‌سی، حدود ۱۰ سیب مورد نیاز است.

جواب کار در کلاس صفحه ۱۳۱ ریاضی پنجم دبستان

زهرا از پنج نفر از دوستانش پرسید که هر کدام چند کتاب داستان دارند. او پاسخ دوستانش را در یک جدول نوشته است.

الف) برای محاسبه میانگین تعداد کتاب‌ها:
ابتدا تعداد کل کتاب‌ها را حساب می‌کنیم:
۵ + ۷ + ۳ + ۹ + ۶ = ۳۰
سپس تعداد کل کتاب‌ها را بر تعداد دوستان تقسیم می‌کنیم:
۳۰ ÷ ۵ = ۶
پس میانگین تعداد کتاب‌ها برابر با ۶ است.

ب) چه کسانی کتاب‌های بیشتری از میانگین دارند؟
شادی، مهتاب و نیلوفر.

۲- سه مثال از اعدادی که میانگین آن‌ها ۱۰ می‌شود:
۹، ۱۰ و ۱۱
۵، ۱۰ و ۱۵
۶، ۱۰ و ۱۴

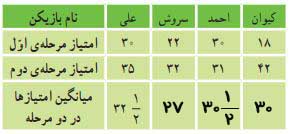
۳- در یک بازی دو مرحله‌ای، امتیاز بچه‌ها به صورت زیر محاسبه می‌شود. جدول را کامل کنید:
مجموع امتیاز مرحله اول و دوم: ۲۲ + ۳۲ = ۵۴
میانگین امتیاز: ۵۴ ÷ ۲ = ۲۷

جواب فعالیت صفحه ۱۳۲ فصل ۷ ریاضی پنجم دبستان

آقای حکیمی یک مزرعه پرورش مرغ دارد که تعداد کمی مرغ در آن نگهداری می‌شود. هر روز، او تخم‌مرغ‌هایی را که مرغ‌ها تولید می‌کنند جمع می‌کند و برای فروش به بازار می‌برد. او همیشه هر روز وزن پنج عدد از این تخم‌مرغ‌ها را اندازه‌گیری و یادداشت می‌کند. تصویری که می‌بینید، یکی از صفحات دفتر یادداشت آقای حکیمی است.

الف) آقای حکیمی برای محاسبه میانگین وزن تخم‌مرغ‌های روز شنبه از یک روش آسان استفاده کرده است. راه‌حلی که او به کار برده را در ادامه کامل کنید.

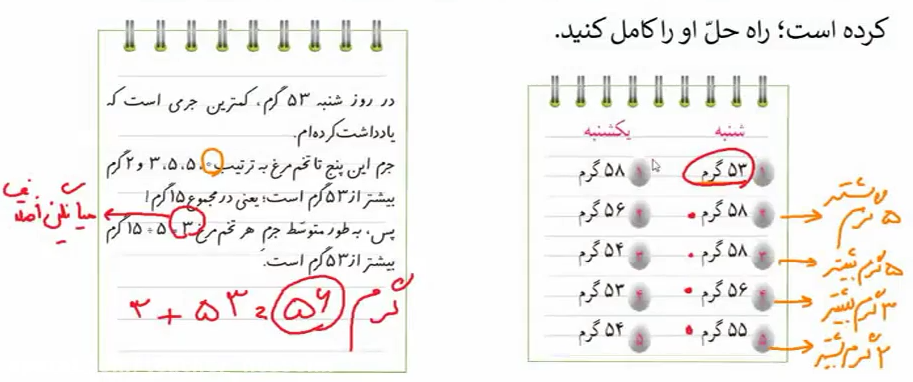
میانگین وزن تخم مرغ‌های روز شنبه را با روش قبلی محاسبه کنید. سپس نتیجه را با پاسخی که از روش جدید به دست می‌آورید، مقایسه کنید.

۳ = ۵ ÷ ۱۵ = ۰ + ۵ + ۵ + ۳ + ۲

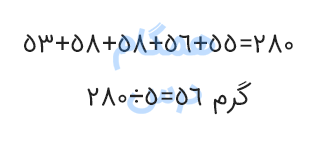
با استفاده از نمودار ستونی ارائه شده، می‌توانید صحت و کارآمدی روش جدید را ثابت کنید.

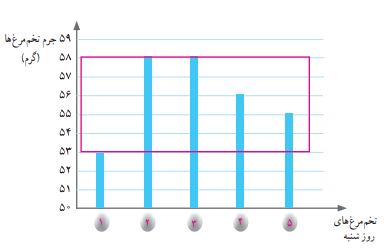
برای محاسبه میانگین داده‌ها از روی نمودار ستونی، کافی است ارتفاع تمام ستون‌ها را با هم برابر کنیم.

ت) میانگین وزن تخم‌مرغ‌های روز یکشنبه را به روشی که خودتان ترجیح می‌دهید محاسبه کنید. پاسخ این سؤال در تصویر بالا نشان داده شده است.

ابتدا تفاوت وزن هر تخم‌مرغ را از سبک‌ترین تخم‌مرغ که ۵۳ گرم است، حساب می‌کنیم. سپس این تفاوت‌ها را با هم جمع می‌زنیم و بر تعداد تخم‌مرغ‌ها که ۵ عدد است، تقسیم می‌کنیم.

میانگین تفاوت‌ها می‌شود ۲ = ۵ ÷ (۱ + ۰ + ۱ + ۳ + ۵)

برای محاسبه میانگین وزن کلی تخم‌مرغ‌ها در روز یکشنبه، این میانگین تفاوت (یعنی ۲) را به وزن سبک‌ترین تخم‌مرغ (یعنی ۵۳) اضافه می‌کنیم.

در نتیجه، میانگین وزن تخم‌مرغ‌ها برابر است با ۵۵ = ۲ + ۵۳ گرم.

جواب تمرین صفحه ۱۳۳ فصل هفتم ریاضی پنجم دبستان

علی مسافت ۴۶۰ سانتیمتر را در ۱۰ قدم پیموده است. میانگین طول هر قدم او چقدر است؟
سانتی متر ۴۶ = ۱۰ ÷ ۴۶۰

دانش‌آموزان کلاس پنجم، کاغذهای دورریخته‌شده در مدرسه را طی یک هفته جمع‌آوری کردند. آن‌ها قصد دارند با کمک این اطلاعات نشان دهند که اگر کاغذهای دورریز در طول سال تحصیلی بازیافت شوند، از قطع شدن چه تعداد درخت جلوگیری می‌شود. داده‌های تقریبی این بررسی در نمودار زیر آورده شده است.

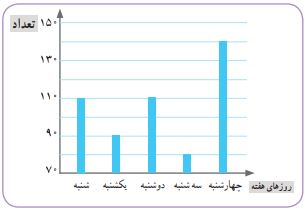
الف) بیشترین تعداد کاغذهای باطله در چه روزی بوده است؟
روز چهارشنبه.

ب) به طور تقریبی، چند تا کاغذ در آن روز دور ریخته شد؟
حدود ۱۴۰ برگ.

پ) میانگین تعداد کاغذهای باطله در هر روز این هفته چقدر است؟
برای محاسبه، اعداد همه روزها را با هم جمع می‌کنیم: ۱۴۰ + ۸۰ + ۱۱۰ + ۹۰ + ۱۱۰ = ۵۳۰
حالا این مجموع را بر تعداد روزها (۵ روز) تقسیم می‌کنیم: ۵۳۰ ÷ ۵ = ۱۰۶
پس به طور میانگین در هر روز ۱۰۶ برگ کاغذ دور ریخته شده است.

۳- محمد در یک بازی ۲۰ بار تاس انداخته و نتیجه هر بار را روی کاغذ نوشته است.

الف) کدام اعداد بیشتر تکرار شده‌اند؟ اعداد ۲ و ۵
ب) کدام عدد کمتر تکرده شده است؟ عدد ۳

۴- میانگین چهار عدد ۱۸، ۱۹، ۲۰ و ۲۷ را محاسبه کنید.
مجموع اعداد:
۸۴ = ۱۸ + ۱۹ + ۲۰ + ۲۷
میانگین:
۲۱ = ۴ ÷ ۸۴

۵- تیم فوتبال مدرسه در ۶ بازی گذشته به ترتیب ۲، ۴، ۳، ۰، ۵ و ۲ گل زده است. در بازی بعدی چند گل باید بزند تا میانگین گل‌هایش در این ۷ بازی برابر ۳ شود؟
فرمول میانگین:
۳ = ۷ ÷ (؟ + ۲ + ۵ + ۰ + ۳ + ۴ + ۲)
طرفین را در ۷ ضرب می‌کنیم:
۲۱ = (؟ + ۲ + ۵ + ۰ + ۳ + ۴ + ۲)
جمع اعداد شش بازی اول:
۱۶ = ۲ + ۵ + ۰ + ۳ + ۴ + ۲
بنابراین:
۲۱ = ؟ + ۱۶
؟ = ۵

۶- میانگین چهار عدد مختلف برابر ۱۰ است.
الف) مجموع این چهار عدد چقدر است؟
۴۰ = ۴ × ۱۰

ب) اگر بزرگترین عدد ۲۵ و کوچکترین عدد ۲ باشد، دو عدد دیگر چه اعدادی می‌توانند باشند؟
مثال‌هایی از دو عدد دیگر:
۱۰ و ۳، ۴ و ۹، ۵ و ۸، ۶ و ۷

جواب فعالیت صفحه ۱۳۴ ریاضی پنجم دبستان

۱- ما در زندگی روزمره، برای نشان دادن احتمال رخ دادن یک اتفاق، از واژه‌های مختلفی استفاده می‌کنیم. مثلاً می‌گوییم: «شاید»، «احتمال دارد» یا «ممکن است».
مثلاً:
پردیدن من به اندازهٔ پنجاه متر، تقریباً غیرممکن است.
اینکه پدرم فردا به مدرسه بیاید، احتمال کمی دارد.
شانس بردن یا باختن در مسابقهٔ بعدی، مساوی است.
از آنجا که خیلی تلاش کرده‌ام، به احتمال زیاد می‌توانم مسئلهٔ بعدی را حل کنم.
یک مربع بدون شک چهار ضلع دارد.

حالا شما هم با استفاده از این واژه‌ها جمله بسازید:
ممکن است فردا باران ببارد.
احتمال کمی دارد که ساعت ۱۰ صبح خواب باشم.
مطمئناً جمعه به مدرسه نمی‌روم.
شاید امروز با مادرم به بازار رفته باشم.
اگر سکه بیندازم، شانس آمدن «پشت» یا «رو» برابر است.
بدون شک امروز چهارشنبه است.
امشب ممکن است برای ناهار قرمه‌سبزی بخوریم.

۲- یک پاکت بردارید و تعدادی دکمه کاملاً شبیه به هم از نظر شکل و اندازه، با رنگ‌هایی که در تصویر می‌بینید، داخل آن قرار دهید. (اگر دکمه ندارید، می‌توانید دایره‌های هم‌اندازه از مقوا ببرید و رنگ کنید.) حالا بدون نگاه کردن داخل پاکت، یک دکمه از آن بیرون بکشید.
الف) برای هر اتفاق، مانند نمونه، روی نوار احتمال، علامت بزنید.

برای این کار، پاکت را نگاه نکنید و فقط دستتان را داخل آن ببرید. سپس یک دکمه بردارید.
رنگ دکمه‌ای که بیرون آورده‌اید را در جدول روبه‌رو، با کشیدن یک خط ثبت کنید.
بعد، دکمه را دوباره داخل پاکت بگذارید.
این کار را بیست بار تکرار کنید و در پایان، تعداد دفعاتی که هر رنگ دیده شده را در جدول بنویسید.

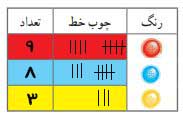
نتایجی که هر یک از شما به دست آورده‌اید را در کنار هم بگذارید و همه را در جدولی که مقابلتان است وارد کنید.
برای مثال، در یک کلاس با سی دانش‌آموز این کار را انجام دهید.

نتایج به‌دست‌آمده را با پاسخ‌هایی که در بخش الف نوشته بودید مقایسه کنید.
می‌بینیم که در هر دو حالت، شانس بیرون آمدن مهره‌ها یکسان است.

جواب کار در کلاس صفحه ۱۳۵ ریاضی پنجم دبستان

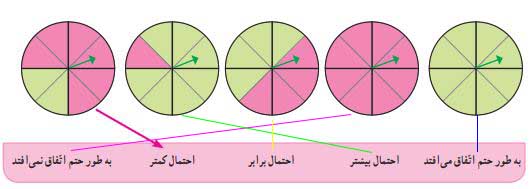
برای هر یک از چرخنده‌های نشان داده شده، عقربه را می‌چرخانیم.
احتمال اینکه عقربه روی رنگ سبز بایستد، با کدام عبارت مشخص می‌شود؟ آن را مانند نمونه نشان دهید.

با استفاده از رایانه، یک چرخنده شبیه به شکل زیر ساخته‌ایم و آن را ده هزار بار چرخانده‌ایم. نتایج این آزمایش در جدول زیر نشان داده شده است.

الف) لطفاً اعداد را به صورت تقریبی در جدول وارد کنید و نمودار دایره‌ای مربوط به این اطلاعات را تکمیل نمایید.

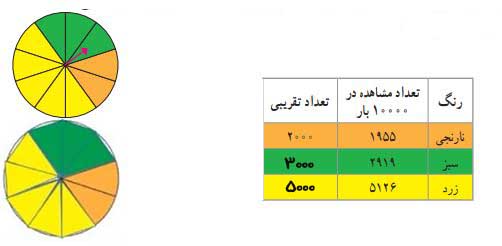
بین نمودار دایره‌ای و چرخنده چه نقطه‌های مشترکی می‌بینید؟
این دو نمودار کاملاً شبیه به هم هستند.

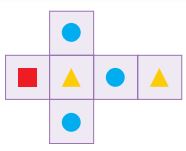
۳- با استفاده از الگویی که در زیر می‌بینید، یک تاس مکعبی درست می‌کنیم. اگر این تاس را پرتاب کنیم، کدام شکل نسبت به بقیه، احتمال بیشتری برای دیده شدن دارد؟
دایره آبی رنگ، چون تعداد آن از بقیه شکل‌ها بیشتر است.

جواب فعالیت صفحه ۱۳۶ ریاضی پنجم دبستان

یک تیم دو نفره بسازید. سپس یک سکه و یک مهره برداشته و این بازی را شروع کنید.

در کنار یکدیگر بنشینید و مشخص کنید که چه کسی در سمت راست و چه کسی در سمت چپ قرار دارد. مهره را دقیقاً در خانه وسط بگذارید.

سکه را پرتاب کنید. اگر شیر آمد، مهره را یک خانه به راست حرکت دهید و اگر خط آمد، مهره را یک خانه به چپ ببرید.

برنده بازی کسی است که مهره زودتر به خانه او برسد.

پس از پایان، نتیجه بازی را در کلاس بیان کنید و آن را با نتایج گروه‌های دیگر مقایسه کنید.

این بازی یک بازی شانسی محسوب می‌شود. در بازی‌های شانسی، اگر شانس برنده شدن همه بازیکنان برابر باشد، بازی عادلانه خواهد بود.

به نظر شما این بازی عادلانه است؟

بله، چون احتمال برنده شدن هر دو بازیکن یکسان است.

جواب کار در کلاس صفحه ۱۳۶ ریاضی پنجم دبستان

۱- بازی‌های عادلانه را با علامت ✔️ نشان دهید و برای بازی‌های ناعادلانه، مشخص کنید کدام بازیکن شانس بیشتری برای بردن دارد.

الف) یک سکه می‌اندازیم؛ اگر شیر آمد، بازیکن اول برنده است و اگر خط آمد، بازیکن دوم.
✔️ عادلانه است.

ب) تاس می‌اندازیم؛ اگر عدد ۱، ۲، ۳ یا ۴ بیاید، بازیکن اول می‌برد و در غیر این صورت، بازیکن دوم.
این بازی ناعادلانه است و احتمال بردن بازیکن اول بیشتر است.

پ) عقربه چرخان مقابل را می‌چرخانیم؛ اگر روی رنگ سبز توقف کند، بازیکن اول برنده است و اگر روی رنگ بنفش بایستد، بازیکن دوم.
✔️ عادلانه است.

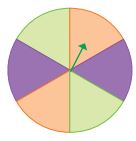
در بازی اول، عقربه‌ای داریم که می‌چرخد. اگر عقربه روی رنگ سبز بایستد، بازیکن اول برنده می‌شود و در غیر این صورت، بازیکن دوم برنده خواهد بود. این بازی منصفانه نیست، چون شانس برنده شدن بازیکن دوم بیشتر است.

در بازی دوم، ما ۲۰ تیله داریم که می‌خواهیم داخل یک کیسه بگذاریم. سپس بدون نگاه کردن به داخل کیسه، یک تیله بیرون می‌آوریم. اگر تیله آبی بود، بازیکن اول برنده است و اگر سبز بود، بازیکن دوم برنده می‌شود. حالا باید ببینیم چند تیله آبی و چند تیله سبز در کیسه بگذاریم تا بازی عادلانه شود.

برای اینکه بازی عادلانه باشد، باید تعداد تیله‌های آبی و سبز با هم برابر باشد. پس از هر رنگ ۱۰ تیله در کیسه قرار می‌دهیم.

جواب تمرین صفحه ۱۳۷ ریاضی پنجم دبستان

مسعود با چند تا از دوستانش سرگرم بازی بودند. در حین بازی، مسعود نتیجه‌ای که تاس‌ها نشان می‌دادند را روی کاغذ می‌نوشت. خلاصه‌ی چیزهایی که مسعود یادداشت کرده بود، داخل یک جدول نوشته شده است.

الف) در این بازی، چند بار تاس انداخته‌اند؟
تعداد کل دفعات تاس‌اندازی ۳۰ بار بوده است. این عدد از جمع اعداد زیر به دست می‌آید:
۳۰ = ۷ + ۸ + ۴ + ۱ + ۷ + ۳

ب) کدام عدد بیشتر از بقیه ظاهر شده است؟
عدد ۵ بیشتر از سایر اعداد دیده شده است.

پ) کدام دو عدد به تعداد یکسان دیده شده‌اند؟
اعداد ۲ و ۶ به تعداد برابر ظاهر شده‌اند.

۲ــ اگر یک سکه را ۵ بار پرتاب کنیم، آیا ممکن است هر ۵ بار روی بیاید؟
بله، این امکان وجود دارد.

۳ــ می‌خواهیم عقربه چرخان زیر را بچرخانیم. کدام یک از این دو نفر درست می‌گوید؟ چرا؟

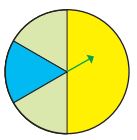
سینا: شانس اینکه عقربه روی رنگ سبز بایستد، از بقیه رنگ‌ها بیشتر است؛ چون دو بخش از چرخ، سبز است، اما فقط یک قسمت زرد و یک قسمت آبی دارد. این حرف اشتباه است. ❌

مینا: احتمال توقف عقربه روی رنگ زرد، از سایر رنگ‌ها بیشتر است؛ چون قسمت زردِ چرخنده، بزرگ‌تر از بخش‌های مربوط به رنگ‌های دیگر است. این حرف درست است. ✅

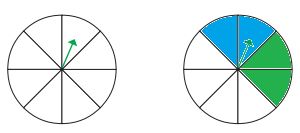
۴ــ چرخنده‌ی زیر را طوری رنگ کنید که:
– شانس ایستادن عقربه روی آبی و سبز یکسان باشد.
– احتمال توقف عقربه روی رنگ سفید، از هر رنگ دیگری بیشتر باشد.

 جواب فرهنگ نوشتن صفحه ای  ۱۳۹ و ۱۳۸ ریاضی پنجم

۱- یک نمونه برای نمایش اطلاعات با نمودار خط شکسته، ثبت تغییرات دمای هوا در طول یک هفته است. میزان دمای محل زندگی خود را در یک هفته یادداشت کنید و سپس آن را با یک نمودار خط شکسته نمایش دهید.

۲- برای محاسبه میانگین چهار عدد، ابتدا آن‌ها را با هم جمع می‌کنیم و سپس حاصل را بر عدد ۴ تقسیم می‌کنیم. به عنوان مثال، برای اعداد ۲۱، ۲۷، ۱۳ و ۱۵، محاسبات به این صورت است:
جمع اعداد: ۷۶ = ۲۱ + ۲۷ + ۱۳ + ۱۵
میانگین: ۱۹ = ۴ ÷ ۷۶

۳- پنج عددی بنویسید که میانگین آن‌ها برابر با ۱۲ باشد. (برای این سؤال سه جواب مختلف ارائه دهید.)
مجموع پنج عدد باید برابر با ۶۰ باشد، زیرا: ۶۰ = ۵ × ۱۲
نمونه‌هایی از این اعداد:
(۸، ۱۰، ۱۲، ۱۴، ۱۶)
(۴، ۹، ۱۲، ۱۵، ۲۰)
(۱۲، ۱۲، ۱۲، ۱۲، ۱۲)

۴- سه عدد متوالی بنویسید که میانگین آن‌ها ۱۵ باشد. (می‌توانید پاسخ را حدس بزنید و سپس بررسی کنید.)
نمونه‌هایی از این اعداد:
(۱۴، ۱۵، ۱۶)
(۱۵، ۱۵، ۱۵)

۵- برای آسفالت کردن کوچه‌ای به عرض ۵ متر و طول ۱۰۰ متر، از ۵۰ تن آسفالت استفاده شده است. به طور متوسط، در هر مترمربع چند کیلوگرم آسفالت به کار رفته است؟
مساحت کوچه: ۵۰۰ مترمربع = ۱۰۰ × ۵
مقدار آسفالت بر حسب کیلوگرم: ۵۰۰۰۰ کیلوگرم = ۱۰۰۰ × ۵۰
مقدار آسفالت در هر مترمربع: ۱۰۰ کیلوگرم = ۵۰۰ ÷ ۵۰۰۰۰

۶- ثنا در سه مرحله از یک مسابقه به ترتیب ۱۸، ۱۵ و ۲۷ امتیاز کسب کرده است.
الف) میانگین امتیازهای او را محاسبه کنید.
جمع امتیازها: ۶۰ = ۱۸ + ۱۵ + ۲۷
میانگین: ۲۰ = ۳ ÷ ۶۰

ب) در مرحله چهارم، چه امتیازی باید کسب کند تا میانگین امتیازهایش تغییر نکند؟
برای حفظ میانگین ۲۰، مجموع امتیازهای چهار مرحله باید برابر با ۸۰ باشد: ۸۰ = ۴ × ۲۰
امتیاز مرحله چهارم: ۲۰ = ۶۰ – ۸۰

۷- مینا، نماینده کلاس، تعداد غایبان هر روز در هفته گذشته را یادداشت کرده است. میانگین تعداد غایبان در هر روز را محاسبه کنید.

برای محاسبه میانگین غایب‌ها، ابتدا تعداد غایب‌های هر روز را با هم جمع می‌کنیم:

۵ = ۰ + ۱ + ۳ + ۰ + ۱ = مجموع روزهای غیبت

سپس این مجموع را بر تعداد روزها تقسیم می‌کنیم تا میانگین به دست آید:

۱ = ۵ ÷ ۵ = میانگین تعداد غایب‌ها

یعنی به طور متوسط، در هر روز یک نفر غایب بوده است.

حالا برای محاسبه میانگین اعداد زیر:
۰/۷ ، ۱/۱ ، ۲/۷ ، ۳/۵

ابتدا آن‌ها را با هم جمع می‌کنیم:
۸ = ۰/۷ + ۱/۱ + ۲/۷ + ۳/۵ = مجموع اعداد

سپس مجموع را بر تعداد اعداد (که ۴ تا است) تقسیم می‌کنیم:
۲ = ۴ ÷ ۸ = میانگین اعداد

در یک مسابقه والیبال، دو تیم ۶ نفره از دانش‌آموزان با هم بازی می‌کنند. قد بازیکنان هر تیم در جدول نوشته شده است.

الف) کوتاه‌ترین بازیکن در تیم مدرسه فجر است که قدش ۱۲۰ سانتی‌متر است.
ب) بلندترین بازیکن در تیم مدرسه آزادی است که قدش ۱۵۵ سانتی‌متر است.

پ) برای مقایسه دو تیم، میانگین قد بازیکنان هر تیم را محاسبه می‌کنیم.

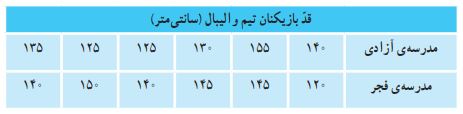
مدرسه آزادی:
جمع قد بازیکنان: ۱۳۵ + ۱۲۵ + ۱۳۵ + ۱۳۰ + ۱۵۵ + ۱۴۰ = ۸۱۰
میانگین قد: ۸۱۰ تقسیم بر ۶ = ۱۳۵

مدرسه فجر:
جمع قد بازیکنان: ۱۲۰ + ۱۴۵ + ۱۴۵ + ۱۴۰ + ۱۵۰ + ۱۴۰ = ۸۴۰
میانگین قد: ۸۴۰ تقسیم بر ۶ = ۱۴۰

همانطور که می‌بینید، میانگین قد بازیکنان تیم والیبال مدرسه فجر، ۵ سانتیمتر از میانگین قد بازیکنان مدرسه آزادی بیشتر است. این یعنی به طور میانگین، هر بازیکن در تیم مدرسه فجر، ۵ سانتیمتر از هر بازیکن در تیم مدرسه آزادی بلندتر است.

۸- ما ۵ تیله سفید و ۵ تیله نارنجی داریم. می‌خواهیم ۴ تیله را داخل یک کیسه بریزیم و سپس بدون نگاه کردن، یک تیله از آن بیرون بکشیم.
در هر حالت، مشخص کنید چند تیله سفید و چند تیله نارنجی باید در کیسه بریزیم تا تیله‌ای که بیرون می‌آوریم:
الف) به احتمال زیاد سفید باشد. (پاسخ: ۴ تیله سفید و ۰ تیله نارنجی)
ب) احتمال سفید بودن آن کمتر از نارنجی بودنش باشد. (پاسخ: ۱ تیله سفید و ۳ تیله نارنجی)
پ) احتمال سفید یا نارنجی بودن آن برابر باشد. (پاسخ: ۲ تیله سفید و ۲ تیله نارنجی)
ت) قطعاً سفید نباشد. (پاسخ: ۰ تیله سفید و ۴ تیله نارنجی)

۹- می‌خواهیم با استفاده از الگوی داده شده، یک تاس مکعبی درست کنیم. روی هر وجه آن یکی از شکل‌های ☹️، 😐، یا 😊 را رسم می‌کنیم؛ به طوری که وقتی تاس را می‌اندازیم، شانس دیدن شکل 😊 از بقیه بیشتر و شانس دیدن شکل ☹️ از بقیه کمتر باشد.
برای این کار می‌توانیم: ۳ وجه را به شکل 😊، ۲ وجه را به شکل 😐 و ۱ وجه را به شکل ☹️ در نظر بگیریم.