تحقیق در مورد ذوزنقه، ویژگی و انواع آن

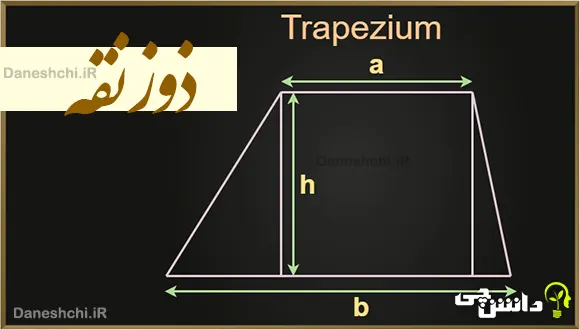
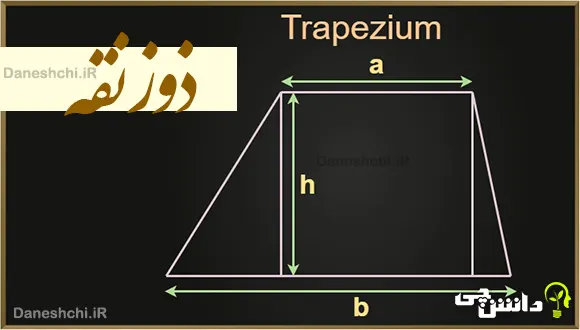
ذوزنقه یک شکل چهارضلعی است که تنها دو ضلع آن با هم موازی هستند. این دو ضلع موازی، معمولاً “قاعده” نامیده می‌شوند. دو ضلع دیگر آن که موازی نیستند، “ساق” نام دارند.

انواع مختلفی از ذوزنقه وجود دارد:
* **ذوزنقه متساوی‌الساقین:** در این نوع، دو ساق با هم برابرند و زوایای هر قاعده نیز با هم مساوی هستند.
* **ذوزنقه قائم‌الزاویه:** این ذوزنقه دو زاویه قائمه (۹۰ درجه) دارد.

برای محاسبه مساحت ذوزنقه از این فرمول استفاده می‌کنیم:
(مجموع دو قاعده × ارتفاع) ÷ ۲

به زبان ساده، میانگین دو قاعده را محاسبه کرده و در ارتفاع ضرب می‌کنیم. ارتفاع ذوزنقه، فاصله عمودی بین دو قاعده موازی است.

در هندسه، تعریف‌های گوناگونی از شکل ذوزنقه ارائه شده است. بعضی از کتاب‌ها آن را به عنوان یک چهارضلعی با دو ضلع موازی می‌شناسند و آن را در دسته متوازی‌الاضلاع قرار می‌دهند، در حالی که برخی دیگر آن را جدا از متوازی‌الاضلاع در نظر می‌گیرند. پروکلوس، فیلسوف و ریاضیدان یونانی، که روش‌های متفاوتی نسبت به فیثاغورث در اثبات قضیه‌های هندسی داشت، چهارضلعی‌ها را به دو گروه متوازی‌الاضلاع و غیر متوازی‌الاضلاع تقسیم کرده است. در این نوشته، با بررسی ویژگی‌ها و گونه‌های مختلف ذوزنقه، بیشتر با این چهارضلعی خاص و جالب آشنا خواهیم شد.

تعریف ذوزنقه

کلمه ذوزنقه از دو بخش تشکیل شده است. بخش اول “ذو” به معنای دارا و صاحب است و بخش دوم “زنق” به معنی چانه یا کجی می‌باشد. چون این شکل شبیه به چانه است، به آن ذوزنقه می‌گویند که یعنی “چانه‌دار” یا “دارای انحراف”.

در هندسه، ذوزنقه یک شکل چهارضلعی بسته است که چهار زاویه دارد. در این شکل، دو ضلع با هم موازی هستند و دو ضلع دیگر موازی نیستند و در مقابل هم قرار گرفته‌اند.

به شکل ذوزنقه در پایین نگاه کنید. اضلاع آن AB، BC، CD و AD هستند. در اینجا AB با CD موازی است و به آن‌ها قاعده‌های ذوزنقه می‌گوییم. اما AD و BC با هم موازی نیستند و به آن‌ها ساق‌های ذوزنقه گفته می‌شود. h نیز نشان‌دهنده ارتفاع ذوزنقه است. شما می‌توانید برای نامگذاری ذوزنقه از حروف دیگر هم استفاده کنید؛ مثلاً به جای h از حرف “ب” برای نشان دادن بلندی شکل کمک بگیرید.

ویژگی های یک ذوزنقه

هر شکل چهارضلعی ویژگی‌های منحصر به فردی دارد که باعث می‌شود بتوان آن را از دیگر شکل‌ها تشخیص داد. این ویژگی‌ها در واقع مشخصات هندسی آن شکل هستند.

ذوزنقه یک شکل هندسی دو بعدی است.
در ذوزنقه، دو ضلع که به آن‌ها پایه می‌گوییم، با هم موازی هستند.
دو زاویه‌ای که در کنار هر ضلع غیرموازی قرار دارند، اگر با هم جمع شوند، حاصل ۱۸۰ درجه خواهد بود.
ذوزنقه از دو ضلع موازی و دو ضلع غیرموازی تشکیل شده است.
اگر تمام زوایای داخل ذوزنقه را با هم جمع کنیم، همیشه به عدد ۳۶۰ درجه می‌رسیم.
ذوزنقه دارای دو قطر است. برخلاف بعضی از چهارضلعی‌های دیگر، این دو قطر با هم برابر نیستند. طول این قطرها به اندازه‌ی پایه‌ها و زوایای ذوزنقه بستگی دارد. این دو قطر همیشه یکدیگر را قطع می‌کنند.

انواع ذوزنقه

ذوزنقه‌ها را می‌توان بر اساس ویژگی‌های اضلاع و زوایای آن‌ها به سه گروه تقسیم کرد.

ذوزنقه مختلف الاضلاع

ذوزنقه‌ای که هر چهار ضلع آن طول متفاوتی دارند و هیچ‌کدام با هم مساوی نیستند، یک ذوزنقه مختلف‌الاضلاع نامیده می‌شود. در این نوع ذوزنقه، اندازه‌ی زاویه‌ها نیز با هم تفاوت دارد. برای اینکه راحت‌تر آن را به خاطر بسپارید، می‌توانید از اصطلاح “ذوزنقه نامنظم” استفاده کنید.

ذوزنقه متساوی الساقین

در یک ذوزنقه متساوی‌الساقین، دو ساق با هم مساوی هستند. یعنی دو ضلعی که با هم موازی نیستند، طول یکسانی دارند. به همین دلیل، این نوع ذوزنقه را می‌توان به عنوان یک ذوزنقه منظم در نظر گرفت.

ذوزنقه قائم الزاویه

ذوزنقه‌ای که یکی از ساق‌های آن با هر دو پایه زاویه قائمه (۹۰ درجه) بسازد، ذوزنقه قائم‌الزاویه نامیده می‌شود. این نوع ذوزنقه نیز مانند ذوزنقه معمولی، اضلاع نابرابر دارد. تفاوت اصلی در این است که در ذوزنقه قائم‌الزاویه، دو زاویه راست (۹۰ درجه) وجود دارد.

فرمول‌های مهم ذوزنقه

برای محاسبه مساحت و محیط ذوزنقه، از فرمول‌های مشخصی استفاده می‌شود. این فرمول‌ها به شما کمک می‌کنند تا به راحتی اندازه‌های مورد نظر را پیدا کنید.

**مساحت ذوزنقه:**
برای به دست آوردن مساحت، کافی است جمع دو قاعده را محاسبه کنید، سپس حاصل را در ارتفاع ضرب کرده و بر دو تقسیم کنید.
فرمول آن به این صورت است:
`مساحت = (مجموع دو قاعده × ارتفاع) ÷ ۲`

**محیط ذوزنقه:**
محیط ذوزنقه از جمع اندازه هر چهار ضلع آن به دست می‌آید.
فرمول آن نیز بسیار ساده است:
`محیط = مجموع همه ضلع‌ها`

مساحت

برای محاسبهٔ مساحت ذوزنقه، ابتدا باید دو قاعدهٔ آن را با هم جمع کنید. سپس حاصل این جمع را تقسیم بر دو کنید تا میانگین دو قاعده به دست آید. در آخر، این میانگین را در ارتفاع ذوزنقه ضرب کنید.
بنابراین مساحت برابر است با:
½ × (مجموع دو قاعده) × ارتفاع
یا به عبارتی:
((AB + CD) ÷ ۲) × h

محیط

برای محاسبه محیط ذوزنقه، کافی است اندازه هر چهار ضلع آن را با هم جمع کنید. بنابراین، محیط این شکل برابر خواهد بود با مجموع اندازه‌های AB و BC و CD و AD.

میانه مرکزی

خط میانه در یک ذوزنقه، پاره‌خطی است که وسط دو ساق آن را به هم وصل می‌کند. این خط با هر دو قاعده ذوزنقه موازی است و طول آن دقیقاً برابر است با میانگین طول دو قاعده. یعنی اگر طول دو قاعده را با هم جمع کنیم و سپس بر دو تقسیم کنیم، به طول خط میانه می‌رسیم. به عبارت دیگر: (طول قاعده اول + طول قاعده دوم) تقسیم بر دو.

رابطه ذوزنقه و متوازی الاضلاع

در شکل ذوزنقه فقط دو ضلع با هم موازی هستند. اما در متوازی‌الاضلاع هر دو ضلع روبرو با هم موازی می‌باشند.
در متوازی‌الاضلاع، اضلاع روبه‌رویی هم‌طول هستند، در حالی که در ذوزنقه این دو ضلع لزوماً برابر نیستند.
اشکالی مانند مستطیل، مربع و لوزی همگی جزو متوازی‌الاضلاع به شمار می‌روند، اما ذوزنقه به دلیل داشتن تنها دو ضلع موازی، از این دسته خارج است.
بنابراین می‌توان گفت ذوزنقه در واقع یک متوازی‌الاضلاع است که فقط دو ضلع موازی دارد.